Die Simsongerade, von Max Himsel, ehemals JBG
Satz
Wählt man einen Punkt auf dem Umkreis eines Dreiecks und fällt von diesem die Lote auf die Dreiecksseiten, so liegen die Lotfußpunkte auf einer Gerade, der Simsongerade.Beweis
Sei P ein Punkt auf dem Umkreis des Dreiecks ABC. Er befinde sich o.B.d.A. im Winkelfeld von g. Die Lotfußpunkte von P auf AC, AB und BC werden mit Q, R,und S bezeichnet. Um zu zeigen, dass die Punkte Q, R und S auf einer Geraden liegen, genügt es zu beweisen, dass ∡SRB und ∡QRA gleich groß und deshalb Scheitelwinkel einer Geradenkreuzung sind.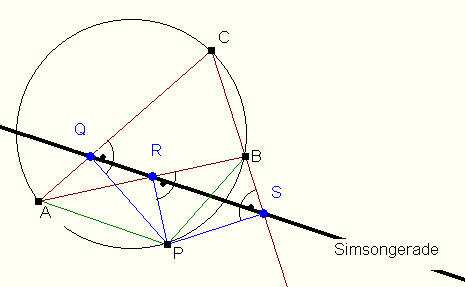
Zunächst wird gezeigt, dass die Vierecke APBC, QPSC, RPSB und APRQ Sehnenvierecke sind:
□APBC ist Sehnenviereck, da P auf dem Umkreis um △ABC liegt.
Bei □QPSC und □RPSB ergänzen sich jeweils zwei gegenüberliegende rechte Winkel zu 180°. In diesem Fall ∡BSP und ∡PQC bzw. ∡BSP und ∡PRB.
Ebenso ist □APRQ ein Sehnenviereck, denn wegen ∡ARP =∡AQP =90° liegen R und Q auf dem Thaleskreis über [AP].
Aus dem Umfangswinkelsatz folgt:
| im □APBC: | (1) ∡BPA | = | 180°- g |
| im □QPSC: | (2) ∡SPQ | = | 180°- g |
| im □RPSB: | (3) ∡QRA | = | ∡QPA |
| im □APRQ: | (4) ∡SRB | = | ∡SPB |
Aus (1) und (2) folgt:
| ∡BPA | = | ∡SPQ | |
| ∡BPQ + ∡QPA | = | ∡SPB + ∡BPQ | |
| -> | ∡QPA | = | ∡SPB |
Zusammen mit (3) und (4) ergibt das ∡QRA = ∡SRB. Damit folgt die Behauptung. #
Weiterführende Links
Zum Umfeld der Wallace-GeradenVortrag von Prof. Dr. O. Giering zur Lehrerfortbildung an der TU-München
De lijn van Simson en een enveloppe
von Dick Klingens